পদার্থবিদ্যা
নিউটনের গতিসূত্র (Newton’s laws of motion)
স্যার আইজ্যাক নিউটন বস্তুর ভর, গতি ও বলের মধ্যে সম্পর্ক স্থাপন করে তিনটি সূত্র প্রকাশ করেন। এটিই নিউটনের গতিসূত্র বা নিউটনের সূত্র নামে পরিচিত।
পদার্থ যে অবস্থায় আছে চিরকাল সেই অবস্থায় থাকতে চাওয়ার যে প্রবণতা বা সেই অবস্থা বজায় রাখতে চাওয়ার যে ধর্ম তাকে জড়তা(inertia) বলে।
ভর (mass) হচ্ছে পদার্থের জড়তার পরিমাপ। অন্য কথায় কোনো একটি বস্তুর তার বেগের পরিবর্তনকে বাঁধা দেয়ার পরিমাপই হচ্ছে ভর।
১৬৮৭ সালে স্যার আইজ্যাক নিউটন তার অমর গ্রন্থ “ন্যাচারালিস ফিলোসোফিয়া প্রিন্সিপিয়া ম্যাথেমেটিকাতে”(Philosophiæ Naturalis Principia Mathematica) বস্তুর ভর, গতি ও বলের মধ্যে সম্পর্ক স্থাপন করে তিনটি সূত্র প্রকাশ করেন। এ তিনটি সূত্র নিউটনের গতিসূত্র (Newtons laws of motion) নামে পরিচিত।
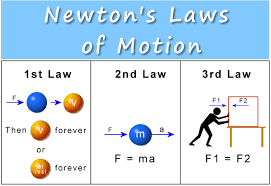
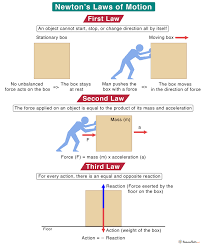
প্রথম সূত্র : (Newton’s First Law) বাহ্যিক বল প্রয়োগে বস্তুর অবস্থার পরিবর্তন করতে বাধ্য না করলে স্থির বস্তু চিরকাল স্থিরই থাকবে এবং গতিশীল বস্তু সমবেগে অর্থাৎ সমদ্রুতিতে সরলপথে চলতে থাকবে।
দ্বিতীয় সূত্র : (Newton’s Second Law) বস্তুর ভরবেগের পরিবর্তনের হার তার ওপর প্রযুক্ত বলের সমানুপাতিক এবং বল যেদিকে ক্রিয়া করে বস্তুর ভরবেগের পরিবর্তনও সেদিকে ঘটে।
তৃতীয় সূত্র : (Newton’s Third Law) প্রত্যেক ক্রিয়ারই একটা সমান ও বিপরীত প্রতিক্রিয়া আছে।
গাণিতিকভাবে নিউটিনের গতিসূত্রগুলোর মধ্যে নিম্নোক্ত উপায়ে পারস্পরিক সম্পর্ক স্থাপন করা যায়।
নিউটনের ২য় সূত্র এবং ১ম সূত্রের মধ্যে সম্পর্ক :
নিউটনের দ্বিতীয় সূত্রকে গাণিতিকভাবে লিখলে আমরা পাই, mv⃗−mv0⃗tαF
∴m(v⃗−v0⃗)tαF
বা, ma⃗=𝑘F⃗, 𝑘=1 হলে
F⃗=ma⃗ , এখানে F⃗ = প্রযুক্ত বল, a⃗=ত্বরণ, v0⃗ =আদিবেগ, 𝑣⃗ = শেষবেগ
বাইরে থেকে বল প্রযুক্ত না হলে F⃗ হয় এবং a⃗ =0 হয়।
কিন্তু বস্তুর ভর শূন্য হয় না তাই 𝑚≠0 সুতরাং a⃗=dv⃗dt=0 অর্থাৎ 𝑣 = ধ্রুবক। ………………
তাই বলা যায় বাহ্যিক বলের ক্রিয়া না থাকলে বেগের কোনো পরিবর্তন হয় না। স্থির বস্তুর স্থির আর গতিশীল বস্তুর গতির কোনো পরিবর্তন হয় না। অর্থাৎ বাহ্যিক বলের অনুপস্থিতিতে বস্তুকণার ভরবেগ(momentum) সব সময় সমান বা ধ্রুব থাকে।
নিউটনের গতির ১ম সূত্র থেকে আমরা জানি বাহ্যিক বল ক্রিয়া না করলে ভরবেগ ধ্রুব থাকে।
অর্থাৎ ভরবেগের সূত্র (momentum formula), P⃗=mv⃗ = ধ্রুবক…………………………………….(4.8)
𝑡 এর সাপেক্ষে ব্যবকলন করে পাই,
dP⃗dt=md(v⃗)dt…………………………………………………………………………………(4.9)
আবার দুটি বস্তুর মধ্যে একটি বস্তু যখন অপরটির উপর বল প্রয়োগ করে তখন লব্ধি ভরবেগের পরিবর্তনের হারের মান সমান ও বিপরীত হয়।
dP1⃗dt=−dP2⃗dt
ddt(m1v1⃗)=−ddt(m2v2⃗)……………………………………………………….……..…………….[4.9(a)]
বা, m1a1⃗=−m2a2⃗ বা, F1⃗=−F2⃗ , অর্থাৎ ক্রিয়া বল= প্রতিক্রিয়া বল।
নিউটনের ২য় সূত্র এবং ৩য় সূত্রের মধ্যে সম্পর্ক :
নিউটনের গতির ২য় সূত্র থেকে আমরা জানি, ভরবেগের পরিবর্তনের হারই হলো প্রযুক্ত বল। ঘাত বল বিবেচনা করলে লেখা যায়, ঘাত বল = ভরবেগের পরিবর্তন। এক্ষেত্রে যে বলের কারণে ঘাত সৃষ্টি হয় বিপরীত ক্রমে সেই বলের কারণে প্রতিঘাত সৃষ্টি হয়। এক্ষেত্রে বলা যায় ক্রিয়া = প্রতিক্রিয়া। ইহাই নিউটনের ৩য় সূত্র।
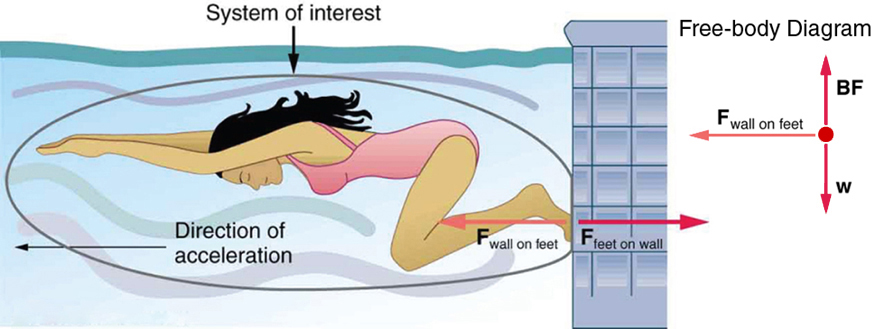
নিউটনের গতিসূত্রের ব্যবহার (Application of Newton’s laws of motion) :
ঘোড়ার গাড়ির চলাচল :
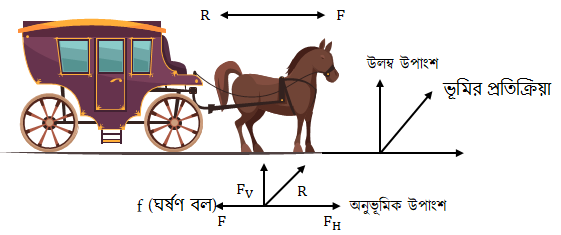
ঘোড়ার গাড়ি রাস্তায় যখন চলে তখন ঘোড়ার কাঁধে বেল্ট বা হাতলের উপর 𝐹 বল প্রয়োগ করে গাড়িটিকে সামনের দিকে নিয়ে যায়। সাথে সাথে গাড়িও ঘোড়াকে পেছনের দিকে সমান ও বিপরীতমুখী 𝐹 বলে টানতে থাকে। স্বাভাবিকভাবে প্রশ্ন করা যায় যে, গাড়িটি সামনের দিকে কী করে এগোয় ? নিচের চিত্রটি লক্ষ কর।

আরোহীসহ গাড়িটি সামনের দিকে এগোয় কী করে? : গাড়িটিকে সামনের দিকে চালাবার জন্য ঘোড়া মাটির উপর তির্যকভাবে বল প্রয়োগ করে। সঙ্গে সঙ্গে মাটি ঘোড়ার উপর সমান ও বিপরীতমুখী প্রতিক্রিয়া বল 𝑅 প্রয়োগ করে। এই বলকে অনুভূমিক দিকে এবং উলম্ব দিকে যথাক্রমে FH এবং FV উপাংশে বিশ্লেষণ করা যায়। উলম্ব উপাংশ FV ঘোড়ার ওজনকে প্রশমিত করে। এখন যদি অনুভূমিক উপাংশ FH ঘোড়ার উপর গাড়ি দ্বারা পেছনের দিকে প্রযুক্ত প্রতিক্রিয়া বল (𝑅) – এর চেয়ে বেশি হয়, তাহলে FH−R বলের ক্রিয়ায় ঘোড়া সামনের দিকে এগিয়ে যায় অর্থাৎ গাড়িটি সামনের দিকে এগিয়ে যায়।
এখন গাড়ির গতি পৃথকভাবে বিবেচনা করলে দেখা যায় যে, এর উপর দুটি বল ক্রিয়া করছে-
(i) মাটির সংস্পর্শে থাকার দরুন চাকার উপর ঘর্ষণ বল 𝑓 ; এই বল গাড়ির গতিকে বাঁধা দেয়।
(ii) ঘোড়া দ্বারা প্রযুক্ত বল 𝐹; এই বল গাড়িকে সামনের দিকে এগিয়ে নিতে চেষ্টা করে।
যখন 𝐹 বলের মান 𝑓 -এর মানের চেয়ে বেশি হয়, তখনই গাড়ি 𝐹−𝑓 বলের ক্রিয়া সামনের দিকে চলতে শুরু করে। এখন চালকসহ গাড়ি যদি সমবেগে চলে অর্থাৎ ত্বরণ শূন্য হলে প্রথম সূত্র অনুযায়ী ওদের উপর ক্রিয়ারত মোট বল শূন্য হবে। সুতরাং FH−F=0 এবং 𝐹−𝑓=0 অর্থাৎ 𝐹= FH =𝑓। চালকসহ গাড়ি ত্বরণ নিয়ে চললে ঘোড়ার ত্বরণ হবে FH−FM এবং গাড়ির ত্বরণ হবে F−fMg , এখানে 𝑀 এবং Mg যথাক্রমে ঘোড়া এবং গাড়ির ভর। FH এবং 𝑓 বল দুটি স্বনিয়ন্ত্রক বল, এদের মান এমনভাবে নিয়ন্ত্রিত হয় যাতে ঘোড়া এবং গাড়ির ত্বরণ সমান হয়। ফলে ঘোড়া ও গাড়ি একসঙ্গে এগিয়ে যায়।
নৌকার গুণ টানা :
মনে করি 𝑀 একটি নৌকা। এর 𝑂 বিন্দুতে গুণ বেঁধে 𝑂𝑅 বরাবর নদীর পাড় দিয়ে 𝐹 বলে টেনে নেওয়া হচ্ছে। বিভাজন পদ্ধতি দ্বারা 𝑂 বিন্দুতে 𝐹 – কে দুটি উপাংশে বিভাজিত করা যায় ; যথা – অনুভূমিক উপাংশ ও উলম্ব উপাংশ [চিত্র]
অনুভূমিক উপাংশ =𝐹 cos 𝜃 , এর দিক 𝑂𝐴 বরাবর
উলম্ব উপাংশ =𝐹 sin 𝜃 , এর দিক 𝑂𝐵 বরাবর।
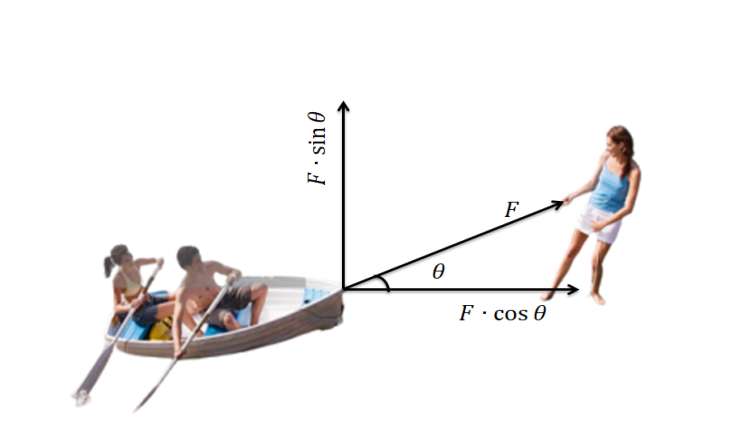
বলের অনুভূমিক উপাংশ 𝐹 cos 𝜃 নৌকাকে সামনের দিকে এগিয়ে নিয়ে যায় এবং উলম্ব উপাংশ 𝐹 sin 𝜃 নৌকাটিকে পাড়ের দিকে টানে। কিন্তু নৌকার হাল দ্বারা উলম্ব উপাংশ 𝐹 sin 𝜃 প্রতিহত করা হয়। গুণ যত লম্বা হবে, 𝜃 -এর মান তত কম হবে ফলে 𝐹 sin 𝜃 – এর মান কম হবে এবং 𝐹 cos 𝜃 -এর মান বেশি হবে। ফলে নৌকা দ্রুত সামনের দিকে এগিয়ে যাবে।
বন্দুক থেকে গুলি ছোঁড়া :
বন্দুক থেকে গুলি ছুঁড়লে গুলিটি প্রচণ্ড বেগে সামনে ছুটে যায়। বন্দুকটি গুলির উপর যদি 𝐹 বল প্রয়োগ করে, তাহলে গুলিটিও বন্দুকের উপর সমান ও বিপরীতমুখী বল প্রয়োগ করে। এই প্রতিক্রিয়া বলের জন্য বন্দুকটিও পেছন দিকে এগিয়ে যায়।
ভরবেগ দিয়েও এর কারণ ব্যাখ্যা করা যায়। গুলি ছোঁড়ার আগে বন্দুক ও গুলি উভয়েই স্থির থাকে। অতএব বন্দুকের ভরবেগ শূন্য এবং গুলির ভরবেগ শূন্য। সুতরাং তাদের মোট আদি ভরবেগ শূন্য। গুলি ছোঁড়ার পর বারুদের বিস্ফোরণের ফলে গুলি একটি বেগে সামনের দিকে যায়। ফলে এটি সামনের দিকে একটি ভরবেগ প্রাপ্ত হয়। ভরবেগের নিত্যতা অনুসারে গুলি ছোঁড়ার পরেও তাদের মোট ভরবেগ শূন্য হবে। ফলে বন্দুককেও গুলির সমান ও বিপরীতমুখী একটি ভরবেগ লাভ করতে হবে। ফলে বন্দুককে অবশ্যই পেছনের দিকে গতিপ্রাপ্ত হতে হবে।

মনে করি 𝑀 ভরের একটি বন্দুক হতে 𝑚 ভরের একটি গুলি v⃗ বেগে বের হয়ে গেল। আবার মনে করি গুলি ছোঁড়ার পর বন্দুকের বেগ = V⃗
∴ গুলি ছোঁড়ার আগে তাদের মোট ভরবেগ =0
গুলি ছোঁড়ার পর তাদের মোট ভরবেগ = বন্দুকের ভরবেগ + গুলির ভরবেগ = MV⃗+mv⃗
কিন্তু ভরবেগের নিত্যতা সূত্র অনুসারে আগের ও পরের ভরবেগ সমান।
{∴MV⃗+mv⃗=0mv⃗=−MV⃗=M(−V⃗)}
অর্থাৎ গুলির ভর × গুলির বেগ = বন্দুকের ভর × বন্দুকের পশ্চাৎ বেগ
এই সমীকরণ থেকে আরো বলা যায়, গুলির বেগ > বন্দুকের পশ্চাৎ বেগ।