শক্তির নিত্যতা সূত্র

সংরক্ষণশীলতা নীতির বিবৃতি

কোনো ব্যবস্থায় কেবল সংরক্ষণশীল বল ক্রিয়া করলে ব্যবস্থার গতিশক্তি ও বিভব শক্তির সমষ্টি সর্বদা ধ্রুব থাকে। অর্থাৎ

গতিশক্তি+বিভবশক্তি=ধ্রুবক

ব্যাখ্যা : কোনো একটি ব্যবস্থায় যদি সংরক্ষণশীল বল ক্রিয়া করে, তবে সেই ব্যবস্থার যান্ত্রিক শক্তি সংরক্ষিত থাকে। সে ক্ষেত্রে ব্যবস্থার গতিশক্তি ও বিভব শক্তির সমষ্টি অর্থাৎ যান্ত্রিক শক্তি ধ্রুব থাকে। যদি ব্যবস্থার গতিশক্তি হ্রাস পায়, তবে বিভব শক্তি বৃদ্ধি পায় আর যদি বিভব শক্তি হ্রাস পায় তবে গতিশক্তি বৃদ্ধি পায়।

কিন্তু তাদের সমষ্টির কোনো পরিবর্তন হয় না। ধরা যাক, কোনো ব্যবস্থার আদি বিভব শক্তি UiUi​ এবং আদি গতিশক্তিKiKi​। ব্যবস্থার উপর সংরক্ষণশীল বল ক্রিয়া করায় ব্যবস্থার শেষে বিভব শক্তি ও গতিশক্তি হলো যথাক্রমে UfUf​ এবং UfUf​। এখন যান্ত্রিক শক্তির সংরক্ষণশীলতা নীতি অনুসারে,

Ui+Ki=Uf+KfUi​+Ki​=Uf​+Kf​

অর্থাৎ $U+K$=ধ্রুবক

অসংরক্ষণশীল বলের ক্ষেত্রে যেমন যদি কোনো ব্যবস্থায় ঘর্ষণ বল ক্রিয়া করে তখন এই সমীকরণ খাটে না, অর্থাৎ যান্ত্রিক শক্তি ধ্রুব থাকে না।

শক্তির নিত্যতার নীতির ব্যবহার

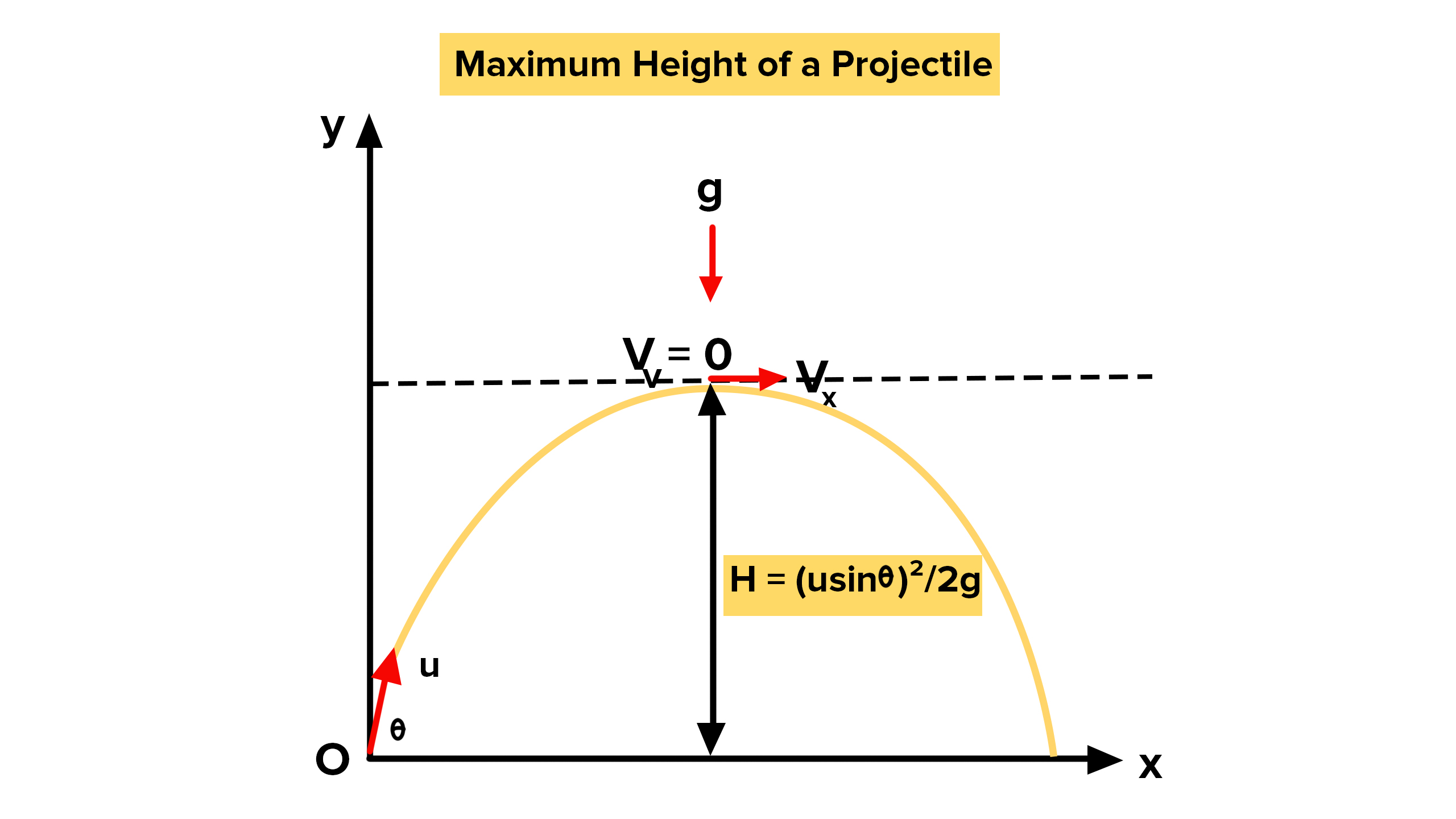
ক. উৎক্ষেপিত বস্তুর সর্বোচ্চ উচ্চতা

একটি বস্তুকে যখন খাড়া উপরের দিকে নিক্ষেপ করা হয় তখন শক্তির নিত্যতার নীতি (Conservation Law of Energy) অনুসারে সবসময় তার মোট যান্ত্রিক শক্তি অর্থাৎ বিভব শক্তি ও গতিশক্তির সমষ্টি ধ্রুব থাকে। ধরা যাক, m ভরের একটি বস্তুকে অভিকর্ষ বলের বিপরীতে খাড়া উপরের দিকে v0v0​ বেগে নিক্ষেপ করা হলো।

নিক্ষেপের মুহূর্তে, বস্তুটি ভূ-পৃষ্ঠে থাকে, ফলে উচ্চতা $h=0$।

সুতরাং নিক্ষেপের সময়

বিভব শক্তি, U1=mgh=0U1​=mgh=0

গতিশক্তি, K1=12mv02K1​=21​mv02

​

∴মোট যান্ত্রিক শক্তি, E1=U1+K1=0+12mv02=12mv02E1​=U1​+K1​=0+21​mv02​=21​mv02​

বস্তুটি যত উপরে উঠতে থাকে, তার বেগ ততো কমতে থাকবে। কমতে কমতে বেগ শূন্য হলে সেটি আবার অভিকর্ষ বলের প্রভাবে নিচে নামতে থাকবে। সুতরাং সর্বোচ্চ উচ্চতায় v=0। ধরা যাক, এ সর্বোচ্চ উচ্চতা hmax⁡hmax​।

সুতরাং সর্বোচ্চ উচ্চতায়

বিভব শক্তি,U2=mghmax⁡U2​=mghmax​

গতিশক্তি, K2=12mv2=0K2​=21​mv2=0

∴মোট যান্ত্রিক শক্তি, E2=U2+K2=mghmax⁡+0=mghmax⁡E2​=U2​+K2​=mghmax​+0=mghmax​

এখন শক্তির নিত্যতার নীতি অনুসারে,

E2=E1∴mghmax⁡=12mv02∴hmax⁡=v022gE2​=E1​∴mghmax​=21​mv02​∴hmax​=2gv02​​​

এ সমীকরণই আমরা তৃতীয় অধ্যায়ে গতির সমীকরণ থেকে পেয়েছি।

খ. সরল ছন্দিত গতি বা সরল দোলন গতির শক্তি

যদি কোনো বস্তুর উপর ক্রিয়াশীল বল একটি নির্দিষ্ট বিন্দু থেকে এর সরণের সমানুপাতিক এবং সর্বদা ঐ বিন্দু অভিমুখী হয়, তাহলে বস্তুর এই গতিকে সরল দোলন গতি বলে।

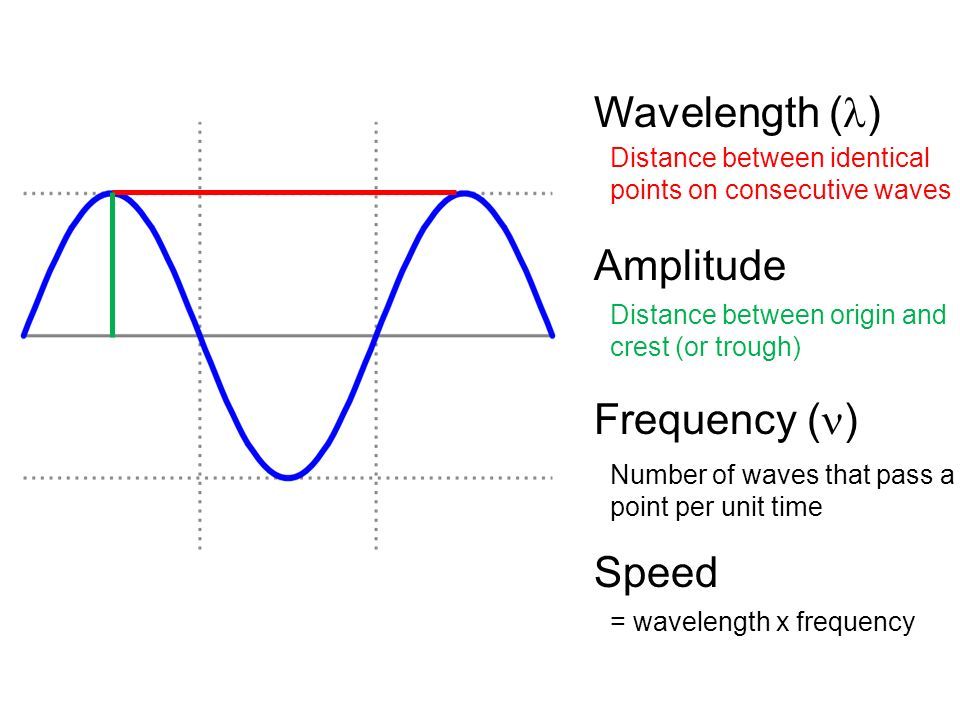
এই নির্দিষ্ট বিন্দুকে সাম্যাবস্থান বা মধ্যাবস্থান বলে এবং সাম্যাবস্থান থেকে যেকোনো একদিকে যে সর্বোচ্চ দূরত্ব অতিক্রম করে তাকে বিস্তার (Amplitude) বলে।

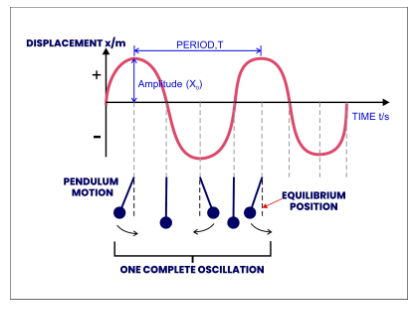
চিত্রে, O হচ্ছে সাম্যাবস্থান এবং NB=A=বিস্তার।

কম্পমান সুরশলাকার গতি, কোনো স্প্রিং-এর এক প্রান্ত দৃঢ় অবস্থানে আটকে অপর প্রান্তে ঝুলানো কোনো বস্তুকে দুলতে দিলে তার গতি সরল দোলন গতি।

কোনো কণার উপর ক্রিয়াশীল বল F এবং সরণ x হলে সরল দোলন গতির ক্ষেত্রে $F=-kx$

এখানে k একটি ধ্রুবক, তাকে বলা হয় বল ধ্রুবক। সরল দোলন গতি সম্পন্ন কোনো কণার সাম্যাবস্থান থেকে x দূরত্বে বিভব শক্তি 12kx221​kx2 এবং কোনো কণার বেগ v হলে তার গতিশক্তি 12mv221​mv2

সরল দোলন গতিসম্পন্ন কোনো কণার দোলনের যে কোনো এক প্রান্তে যেমন C তে বেগ, v=0

এবং সরণ, $x=A$

সুতরাং বিভব শক্তি, U1=12kx2=12kA2U1​=21​kx2=21​kA2

গতিশক্তি, K1=12mv2=0K1​=21​mv2=0

∴মোট যান্ত্রিক শক্তি, E1=U1+K1=12kA2+0=12kA2E1​=U1​+K1​=21​kA2+0=21​kA2

সাম্যাবস্থান থেকে যেকোনো দূরত্ব x-এ অবস্থিত D বিন্দুতে যদি বেগ v হয়,

তাহলে বিভব শক্তি, U2=12kx2=12kA2U2​=21​kx2=21​kA2

গতিশক্তি, K2=12mv2K2​=21​mv2

∴মোট যান্ত্রিক শক্তি, E2=12kx2+12mv2E2​=21​kx2+21​mv2

এখন শক্তির নিত্যতার নীতি (Conservation Law of Energy) অনুসারে D এবং C বিন্দুতে মোট শক্তি সমান।

∴$E2=E1$

12kx2+12mv2=12kA221​kx2+21​mv2=21​kA2

এর থেকে আমরা x দূরত্বে যেকোনো বিন্দুতে বেগ v নির্ণয় করতে পারি,

12mv2=12kA2−12kx2 বা, 12mv2=12k(A2−x2) বা, v2=km(A2−x2)v=km(A2−x2)21​mv2=21​kA2−21​kx2 বা, 21​mv2=21​k(A2−x2) বা, v2=mk​(A2−x2)v=mk​(A2−x2)​​

সরল দোলন গতির ক্ষেত্রে km=ω=mk​​=ω= কৌণিক কম্পাঙ্ক।

∴v=ωA2−x2∴v=ωA2−x2

​সরল দোলকের ক্ষেত্রে যান্ত্রিক শক্তির নিত্যতা

সরল দোলকের আন্দোলনে গতিশক্তি ও বিভব শক্তির রূপান্তর প্রতিনিয়ত ঘটে। আন্দোলনের প্রতি মুহূর্তে গতিশক্তি ও বিভব শক্তির যোগফল সমান থাকে।

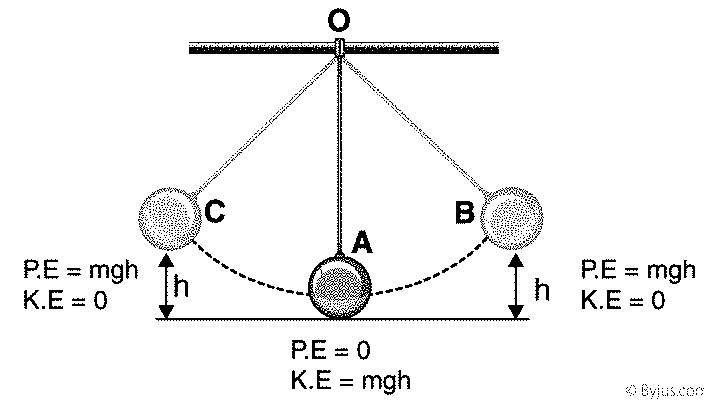
ধরা যাক, OA একটি দোলক এবং B বিন্দু আন্দোলনের ফলে সাম্যাবস্থান থেকে দোলকের সর্বাধিক সরণের অবস্থান, অর্থাৎ B বিন্দুতে দোলকটি মুহূর্তের জন্য থেমে যায় । সুতরাং B বিন্দুতে দোলকের শক্তি সম্পূর্ণরূপে বিভব শক্তি। এখন দোলকের A বিন্দু থেকে B বিন্দুতে যাওয়ার অর্থ খাড়াভাবে A থেকে N বিন্দুতে যাওয়া। সুতরাং B বিন্দুতে দোলকের বিভব শক্তি = $mg\times$খাড়া উচ্চতা$=mg\times AN$।

এখানে m ববের ভর এবং B বিন্দুতে দোলকের গতিশক্তি =0।

অতএব, B বিন্দুতে দোলকের মোট যান্ত্রিক শক্তি $=mg\times AN+0=mg\times AN$

ধরা যাক, আন্দোলিত হয়ে দোলকটি কোনো এক সময় C বিন্দুতে পৌঁছল। এ অবস্থানে দোলকটির বিভব শক্তি ও গতি শক্তি দুই-ই থাকবে।

C বিন্দুতে দোলকের বিভব শক্তি = $mg\times$খাড়া উচ্চতা

=$mg\times AM$

C বিন্দুতে দোলকের গতিশক্তি =12mv2=12m×2gh=mg×NM=mg(AN−AM)=21​mv2=21​m×2gh=mg×NM=mg(AN−AM)

অতএব, C বিন্দুতে দোলকের মোট শক্তি $=mg\times AM+mg(AN-AM)$

$=mg\times AN=B$ বিন্দুতে মোট শক্তি

সুতরাং আন্দোলিত দোলক শক্তির নিত্যতা সূত্র (Conservation Law of Energy) মেনে চলে।