ভর ও শক্তির সম্পর্ক

বিজ্ঞানী আইনস্টাইনের থিওরি অব রিলেটিভিটিতে বলা হয়েছে যে বস্তুর ভর আর শক্তি একই ব্যাপার, এবং ভর m কে যদি শক্তিতে রূপান্তর করা যায় তাহলে সেই শক্তি E এবং এর পরিমাণ হচ্ছে$E=m{c}^2$ যেখানে c হচ্ছে আলোর বেগ। আলোর বেগ ($3\times {10}^{8}m{s}^{-1}$) বিশাল, সেটাকে বর্গ করা হলে আরো বিশাল হয়ে যায়, যার অর্থ অল্প একটু ভরকে শক্তিতে রূপান্তর করতে পারলে আমরা বিশাল শক্তি পেয়ে যাব, নিউক্লিয়ার শক্তিকেন্দ্রে ঠিক এই ব্যাপারটিই করা হয়।

নিউক্লিয়ার শক্তিকেন্দ্রে যেসব জ্বালানি ব্যবহার করা হয় তার একটি হচ্ছে ইউরেনিয়াম 235 এখানে 92টি প্রোটন এবং 143টি নিউট্রন রয়েছে। প্রকৃতিতে এর পরিমাণ খুব কম, মাত্র 0.7%, এর অর্ধায়ু 703,800,000 (704 মিলিয়ন) বছর। এই ইউরেনিয়াম 235 নিউক্লিয়াস খুব সহজেই আরেকটা নিউট্রনকে গ্রহণ করতে পারে (যদি সে নিউট্রনের গতি কম হয়) তখন ইউরেনিয়াম 235 পুরোপুরি অস্থিতিশীল হয়ে যায়, এটা তখন  এবং  এই দুটো ছোট নিউক্লিয়াসে ভাগ হয়ে যায়। তার সাথে সাথে আরো তিনটা নিউট্রন বের হয়ে আসে যেটা নিচের সমীকরণে দেখানো হয়েছে।

কেউ যদি সমীকরণের বাম পাশে যা আছে তার স্তর বের করে এবং সেটাকে ডান পাশে বা আছে তার ভরের সাথে তুলনা করে তাহলে দেখৰে ডান পাশে ভর কম, যেটুকু স্তর কম সেটুকু আসলে $E=m{c}^2$ এর শক্তি হিসেবে বের হয়ে এসেছে।

এই বিক্রিয়ায় যে তিনটি নিউট্রন বের হয়ে এসেছে, তারা আসলে প্রচণ্ড গতিতে বের হয়ে আসে, তাই খুব সহজে অন্য ইউরেনিয়াম () সেগুলো ধরে রাখতে পারে না। কোনোভাবে যদি এগুলোর গতিশন্তি কমানো যায় তাহলে সেগুলো অন্য ইউরেনিয়াম () নিউক্লিয়াসে আটকা পড়ে সেটাকেও ভেঙে দিয়ে আরো কিছু শক্তি এবং আরো তিনটি নতুন নিউট্রন বের করবে। নিউক্লিয়ার শক্তিকেন্দ্রে এই কাজটি করা হয় তাই বের হয়ে আসা নিউট্রনগুলোর গতি কমে আসার পর সেগুলো আবার অন্য নিউক্লিয়াসকে ভেঙে দেয় এবং এভাবে চলতেই থাকে। এই প্রক্রিয়াকে বলে চেইন রি-অ্যাকশন (Chain Reaction ) ।

এই পদ্ধতিতে প্রচণ্ড তাপশক্তি বের হয়ে আসে, সেই তাপশক্তি ব্যবহার করে জলকে বাষ্পীভূত করে সেই বাষ্প দিয়ে টারবাইন ঘুরিয়ে জেনারেটর থেকে বিদ্যুৎ তৈরি করা হয় এবং এ রকম বিদ্যুৎকেন্দ্রকে আমরা বলি নিউক্লিয়ার বিদ্যুৎকেন্দ্র! এরকম একটা বিদ্যুৎকেন্দ্র থেকে খুব সহজেই হাজার মেগাওয়াট বিদ্যুৎ পাওয়া সম্ভব। তবে এই নিউক্লিয়ার বিক্রিয়ার পর যে বর্জ্য পদার্থ তৈরি হয় সেগুলো ভয়ংকর রকম তেজস্ক্রিয়, তাই সেগুলো প্রক্রিয়া করার সময় অনেক রকম সাবধানতা নিতে হয়। নিউক্লিয়ার বিক্রিয়ার পর যে বাড়তি নিউট্রন বের হয় কোনোভাবে সেগুলোকে অন্য কোথাও শোষণ করিয়ে নিতে পারলেই নিউক্লিয়ার বিক্রিয়া বন্ধ হয়ে যায়। নিউট্রনকে শোষণ করার জন্য বিশেষ ধরনের রঙ নিউক্লিয়ার রি-অ্যাক্টরে থাকে যেগুলোকে বলে কন্ট্রোল রড। সেগুলো দিয়ে নিউক্লিয়ার রি-অ্যাক্টরকে নিয়ন্ত্রণ করা হয়।

ভর-শক্তি সম্পর্ক (Mass-energy relation)

আইনস্টাইন-এর ভর-শক্তি সম্পর্ক হলো পদার্থবিজ্ঞানের কালজয়ী সূত্র। আইনস্টাইন আপেক্ষিকতার সাহায্যে এই বিখ্যাত সম্পর্ক নির্ণয় করেন। এই সূত্রকে ভর-শক্তি রূপান্তরের সূত্রও বলে। নিউটনের দ্বিতীয় গতি সূত্র হতে আমরা জানি ভরবেগের পরিবর্তনের হারকে বল বলে। অতএব,

F=ddt( mϑ)F=dtd​( mϑ)  …  …     [8.38]

আপেক্ষিক তত্ত্ব হতে আমরা জানি ভর এবং বেগ উভয়ই পরিবর্তনশীল।

∴F=ddt( mϑ)=mdϑdt+ϑdmdt∴F​=dtd​( mϑ)=mdtdϑ​+ϑdtdm​​…      …           [8.39]

মনে করি বল F বস্তুর dx সরণ ঘটায়। অতএব কৃত কাজ = F.dx। এই কাজ বস্তুটির গতিশক্তি বৃদ্ধির সমান।

∴dEk∴dEk​= F.dx

=(mdϑdt+ϑdmdt)⋅dx=m⋅dϑdt⋅dx+ϑ⋅dmdt⋅dx=mϑ⋅dϑ+ϑ2dm=(mdtdϑ​+ϑdtdm​)⋅dx=m⋅dtdϑ​⋅dx+ϑ⋅dtdm​⋅dx=mϑ⋅dϑ+ϑ2dm​…  …       [8.40]

[∵dxdt=ϑ][∵dtdx​=ϑ]

এখন ভর ও বেগের সম্পর্ক হতে পাই,

m=m01−ϑ2/c2m=1−ϑ2/c2​m0​​ …  …     [8.41]

উভয় পাশে বর্গ করে পাই,

m2=m021−ϑ2/c2 বা, m2=m02c2c2−ϑ2 বা, m2c2−m2ϑ2=m02c2 বা, m2c2=m2ϑ2+m02c2m2=1−ϑ2/c2m02​​ বা, m2=c2−ϑ2m02​c2​ বা, m2c2−m2ϑ2=m02​c2 বা, m2c2=m2ϑ2+m02​c2​ …  …     [8.42]

উভয় পার্শ্বকে অন্তরীকরণ বা অবকলন করে পাই,

2 m⋅dmc2=2 m⋅dmϑ2+2ϑ⋅dϑm22 m⋅dmc2=2 m⋅dmϑ2+2ϑ⋅dϑm2

বা, dm⋅c2=(mϑ⋅dϑ+ϑ2⋅dm)dm⋅c2=(mϑ⋅dϑ+ϑ2⋅dm) …  …     [8.43]

এখন সমীকরণ (8.40) এবং (8.43) হতে পাই,

dmc2=dEk বা,dEk=dmc2dmc2=dEk​ বা,dEk​=dmc2​

উক্ত সমীকরণ হতে প্রমাণিত হয় যে গতিশক্তির পরিবর্তন ভরের পরিবর্তনের সমানুপাতিক

অর্থাৎ dEk∝dmdEk​∝dm

বস্তু যদি স্থির থাকে, তবে $\vartheta =0$ এবং, K.E. = 0

এমতাবস্থায় m = m0m0​। কিন্তু বস্তুর বেগ যখন হয়, তখন ভরের মান হয় m

অতএব সমীকরণ (8.44)-কে সমাকলন করে পাই

∫0EkdEk=∫m0mdm×C2 বা, Ek=c2∫m0mdm বা,Ek=c2[m−m0] বা,Ek=mc2−m0c2∫0Ek​​dEk​=∫m0​m​dm×C2 বা, Ek​=c2∫m0​m​dm বা,Ek​=c2[m−m0​] বা,Ek​=mc2−m0​c2​

এটিই হলো আপেক্ষিকতার গতিশক্তির সমীকরণ।

বস্তু যদি স্থিতিশীল অবস্থায় থাকে, হবে তার মধ্যে যে শক্তি সঞ্চিত থাকে, তাকে স্থির ভর শক্তি (Rest mass energy) বলে এবং এর পরিমাণ =m0c2m0​c2

∴ বস্তুর মোট শক্তি

$\mathrm{E}=$= গতিশক্তি + স্থির ভর শক্তি

বা, E=Ek+m0c2E=Ek​+m0​c2

বা, E=mc2−m0c2+m0c2E=mc2−m0​c2+m0​c2

বা, E=mc2E=mc2

এটিই হলো বিজ্ঞানী আইনস্টাইন-এর ভর-শক্তি সমীকরণ।

স্থির ভর (Rest mass)

আপেক্ষিক তত্ত্ব অনুসারে বস্তুর ভর বেগের সাথে পরিবর্তিত হয়। গতিবেগ আলোর বেগের কাছাকাছি হলে ভর উল্লেখযোগ্যভাবে বৃদ্ধি পায়। এজন্যই বস্তুর নিজস্ব ধর্ম হিসেবে ভরের  উল্লেখ করতে হবে। স্থির অবস্থায় তার ভর নিতে হয়। একেই বস্তুর স্থির ভর বলা হয়। অর্থাৎ একটি বস্তুর অবস্থার ভরই হলো এর স্থির ভর।

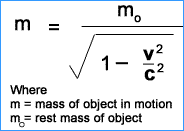
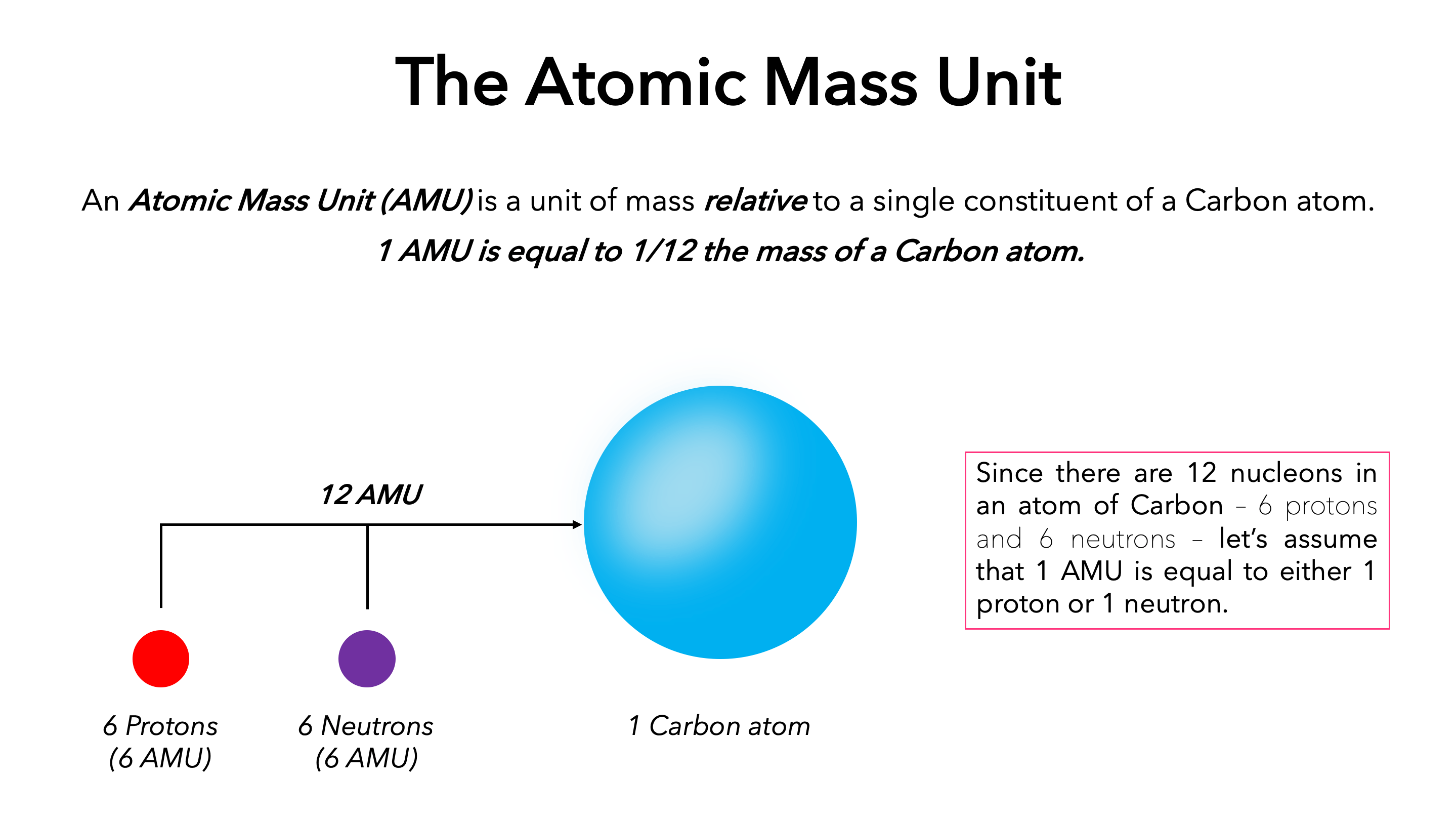
পারমাণবিক ভর একক (Atomic mass unit or amu)

একটি পরমাণুর ভর খুবই নগণ্য। তাই পরমাণুর প্রকৃত ভর বিবেচনা করা হয় না। নিউক্লীয় পদার্থবিজ্ঞানে ভরের প্রচলিত একক হলো পারমাণবিক ভর একক (amu)। 1960 সাল থেকে 6C126​C12 মৌলকে প্রমাণ মৌল ধরে এর সাহায্যে অন্য সকল মৌলের ভর নির্ণয় করা হয়।

এক পারমাণবিক ভর (1 amu) বলতে 6C126​C12 পরমাণুর ভরের 1/12 অংশ বুঝায়।

1 amu = 1.66057×10−27 kg1.66057×10−27 kg

নিউট্রন, প্রোটন প্রভৃতি কণার ভর amu এককে প্রকাশ করা যায়। এই এককে প্রোটন ও নিউট্রনের ভর যথাক্রমে 1.007277 amu ও 1.008665 amu

1 amu  ভরের  সমতুল্য শক্তি =1.66377×10−27(2.998×108)21.6022×1019=933.3×106eV≈933MeV1 amu  ভরের  সমতুল্য শক্তি ​=1.6022×10191.66377×10−27(2.998×108)2​=933.3×106eV≈933MeV

​

• একটি ইলেকট্রনের নিশ্চল ভর 9.028×10−31 kg9.028×10−31 kg। এর শক্তি সমতুল নির্ণয় কর। ইলেকট্রন ভোল্ট (eV)-এ মান কত হবে?

এখানে,

m0=9.02810−31kgm0​=9.02810−31kg c=3×108 ms−1c=3×108 ms−1

ধরি, সমতুল্য শক্তি = E

আমরা পাই,

E=m0c2E=m0​c2

∴ শক্তি সমতুল্য, E=9.028×10−31 kg×(3×108 ms−1)2=8.125×10−14 J=8.125×10−141.6×1019eV=5.078×105eV=0.5078MeVE​=9.028×10−31 kg×(3×108 ms−1)2=8.125×10−14 J=1.6×10198.125×10−14​eV=5.078×105eV=0.5078MeV​

• একটি ইলেকট্রন (নিশ্চল ভর 9.1×10−31 kg)9.1×10−31 kg)) আলোর দ্রুতির 90% দ্রুতিতে চলছে। আইনস্টাইনের আপেক্ষিক তত্ত্ব অনুসারে ইলেকট্রনের গতিশক্তি নির্ণয় কর।

আমরা জানি,

m=m01−v2/c2m=1−v2/c2​m0​​

=9.1×10−311−(0.9cc)2=1−(c0.9c​)2​9.1×10−31​

=2.09×10−30kg=2.09×10−30kg

গতিশক্তি, Ek=(m−m0)c2=(2.09×10−30−9.1×10−31)×(3×108)2=1.062×10−13 JEk​=​(m−m0​)c2=(2.09×10−30−9.1×10−31)×(3×108)2=1.062×10−13 J

​

• ক) 1.6×1061.6×106 eV গতিশক্তিসম্পন্ন ইলেকট্রনের ভর কত ?
• (খ) 12 a. m. u. ভরের সমতুল্য শক্তি (i) eV, (ii) MeV এককে প্রকাশ কর।

 

(ক)

এখানে,

Ek=1.6×106eVEk​=1.6×106eV

=1.6×106×1.6×10−19 J=1.6×106×1.6×10−19 J

c=3×108 ms−1c=3×108 ms−1  m0=9.1×10−31 m0​=9.1×10−31

আমরা জানি,

Ek=(m−m0)c2Ek​=(m−m0​)c2 ∴1.6×106×1.6×10−19=(m−9.1×10−31)(3×108)2∴1.6×106×1.6×10−19=(m−9.1×10−31)(3×108)2

বা, 37.54×10−31=m37.54×10−31=m

∴m=37.54×10−31 kg∴m=37.54×10−31 kg

(খ)

এখানে,

$\mathrm{m}=12\mathrm{a}\cdot \mathrm{m}\cdot \mathrm{u}$

=12×1.66057×10−27 kg=12×1.66057×10−27 kg

c=3×108 ms−1c=3×108 ms−1 1eV=1.6×10−19 J1eV=1.6×10−19 J

আমরা জানি,

(i)  E=mc2E=mc2

=12×1.66057×10−27×(3×108)2=12×1.66057×10−27×(3×108)2 =179.34×10−11 J=179.34×10−11 J =17.934×10−10 J=17.934×10−10 J =17.934×10−101.6×10−19eV=1.6×10−1917.934×10−10​eV =11.2×10−9eV=11.2×10−9eV

(ii) 1MeV=106eV1MeV=106eV

∴E=11.2×109106=11.2×103MeV∴E=10611.2×109​=11.2×103MeV

• একটি বস্তুকণার মোট শক্তি এর স্থির অবস্থার শক্তির দ্বিগুণ। কণাটির দ্রুতি কত?

প্রশ্নানুসারে, mc2=2 m0c2mc2=2 m0​c2

বা, mm0=2m0​m​=2

আবার, m=m01−v2c2m=1−c2v2​​m0​​               বা, mm0=11−v2c2m0​m​=1−c2v2​​1​

বা, 2=11−v2c22=1−c2v2​​1​                       বা, 4=11−v2c24=1−c2v2​1​

বা, 1−v2c2=141−c2v2​=41​

বা, v2c2=1−14c2v2​=1−41​              বা, v2c2=34c2v2​=43​           বা, v2c2=0.75c2v2​=0.75

 

∴v2c2=0.866∴c2v2​=0.866

বা, v=0.0866×3×108=2.598×108 ms−1v=0.0866×3×108=2.598×108 ms−1